electric field is one of the fundamental concepts in physics. It describes the region around a charged object where other charges experience a force. An in-depth understanding of the electric field formula lays the foundation for topics in electromagnetism and is key for solving many physics problems. In this guide, we cover every single point about the electric field formula so that students have all the information they need in one place.
1. What Is an Electric Field?
An electric field is a region of space around a charged object within which a force is exerted on other charges. Think of it as the invisible influence a charge has around itself, much like the gravitational field around a planet.
- When a test charge is placed in an electric field, it experiences a force.
- The direction of the electric field is defined as the direction of the force that a positive test charge would experience.
2. The Basic Electric Field Formula
The electric field (E) at a point in space is defined as the force (F) experienced per unit positive test charge (q):
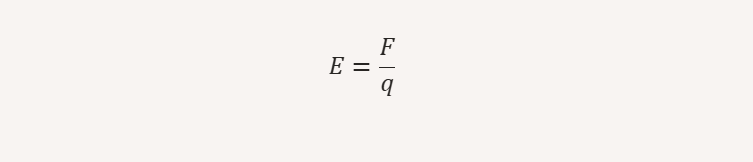
Key Points:
- E (Electric Field) is measured in newtons per coulomb (N/C) or volts per meter (V/m).
- F (Force) is measured in newtons (N).
- q (Charge) is measured in coulombs (C).
When you place a test charge ( q ) in a field, the force it experiences is directly proportional to the strength of the electric field at that point.
3. Electric Field Due to a Point Charge

4. Understanding the Sign Conventions and Direction
- Direction:
The direction of the electric field is conventionally taken as away from positive charges and toward negative charges. - Vector Nature:
The electric field is a vector quantity. This means when multiple charges are present, the net electric field is the vector sum of the individual fields due to each charge.
5. Electric Field Lines
Electric field lines are a visual representation of the field:
- Origins:
Lines originate from positive charges and end at negative charges. - Density:
The density of field lines correlates with the field strength: closer lines mean a stronger field. - Never Cross:
Field lines do not cross because at any given point, the electric field has a unique direction.
6. Uniform and Non-Uniform Electric Fields
- Uniform Electric Field:
- The field strength is constant in magnitude and direction.
- Can be created between two parallel plates.
- Non-Uniform Electric Field:
- The field strength varies with position.
- This is typical around point charges or irregular charge distributions.
7. Practical Applications of the Electric Field
Understanding the electric field formula has real-world relevance:
- Capacitors:
The capacitance of a capacitor depends on the electric field between the plates. - Electronics:
Electric fields govern the behavior of semiconductors and transistors. - Electrostatic Precipitators:
Used in pollution control, they rely on electric fields to remove particles from exhaust gases. - Medical Devices:
Electric fields are harnessed in imaging technologies like MRI machines.
8. Sample Problem and Worked Example

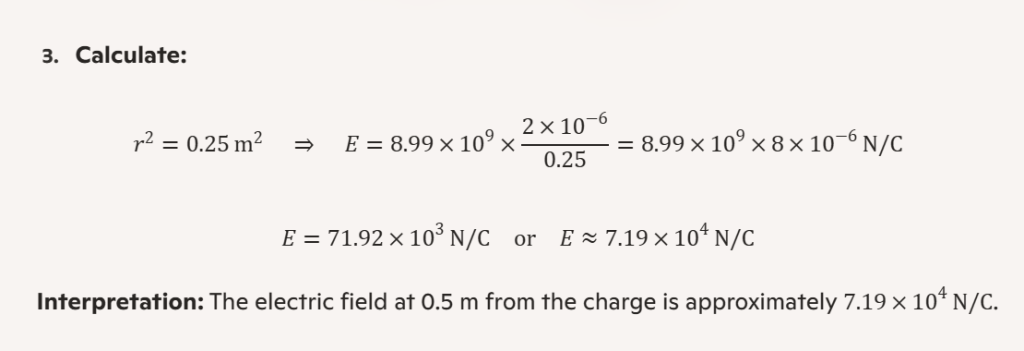
9. FAQs About Electric Field Formula
Q1. What is the most basic definition of an electric field?
A1: An electric field is defined as the force experienced per unit positive charge, given by ( E = \frac{F}{q} ).
Q2. What are the units of the electric field?
A2: The electric field is measured in newtons per coulomb (N/C) or volts per meter (V/m).
Q3. How does the electric field vary with distance?
A3: For a point charge, the electric field decreases as the square of the distance from the charge, described by ( E = k \frac{Q}{r^2} ).
Q4. Why is the electric field a vector quantity?
A4: Because it has both magnitude and direction, and when multiple charges are involved, their fields combine vectorially.
Q5. What is a uniform electric field?
A5: A uniform electric field has the same magnitude and direction at every point, such as the field between two parallel, oppositely charged plates.
Q6. How can I visually represent an electric field?
A6: Electric fields are often represented by field lines. The density and direction of these lines help illustrate the strength and direction of the field.
Conclusion
The electric field formula E = F / q and its application to point charges ( E=k*Q/r2 ) form the backbone of understanding electrostatics. By mastering this formula, along with its concepts, units, and applications, students can tackle a wide range of problems in physics with confidence.

For more expert tips and study resources, keep exploring our articles and join our community at Convex Classes Jaipur, where we make even the most challenging topics easy to grasp.




