Electric flux is a fundamental concept in electromagnetism that may seem abstract at first, but with the right approach, it becomes much easier to grasp. In this article, we focus solely on the unit of electric flux—what it means, how it is derived, and why it’s expressed as N·m²/C (Newtons·meters² per Coulomb) or equivalently as V·m (Volt·meters).
Breaking Down Electric Flux
Electric Flux (Φ_E) quantifies how much of an electric field passes through a specific area. You can picture it as counting the number of “field lines” (imagine them as streams of light) that go through a surface.
The mathematical definition is usually given by:
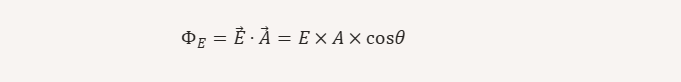
Where:
- E is the electric field strength.
- A is the area through which the field is passing.
- θ (theta) is the angle between the field direction and the line perpendicular (normal) to the surface.
The closer the surface is to being perpendicular to the field, the larger the flux (because cosθ is greater). When the field is parallel to the surface (θ = 90°, cosθ = 0), the flux becomes zero.
Why Is the Unit of Electric Flux N·m²/C?
Let’s break it down step-by-step.
1. Units of the Electric Field (E)
- The electric field is defined as force per unit charge.
- Unit: Newton per Coulomb (N/C) (Alternatively, it can be expressed as Volt per meter (V/m) because 1 V/m = 1 N/C.)
2. Units of the Area (A)
- The area through which the field lines pass is measured in square meters (m²).
3. Combining the Units
When you multiply the unit of the electric field by the unit of the area, you get:
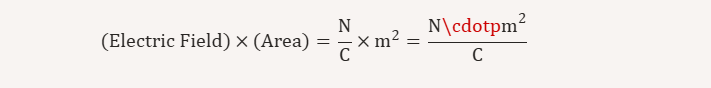
This derivation tells us that electric flux is expressed in Newton-meters squared per coulomb (N·m²/C). Alternatively, recognizing that 1 N/C is the same as 1 V/m, you can also write it as Volt·meters (V·m):
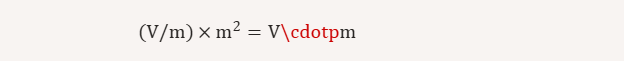
Both units express the same quantity and help ensure that the equations in electromagnetism (like Gauss’s Law) are dimensionally consistent.
Read More NDA Mock Test
Examples to Illustrate the Unit
Let’s look at two examples that illustrate how these units work in practice.
Example 1: Perpendicular Surface
Imagine a uniform electric field with a strength of 120 N/C is passing through a flat surface of 3 m². Since the surface is positioned perpendicular to the electric field (θ = 0°, so cos0° = 1):
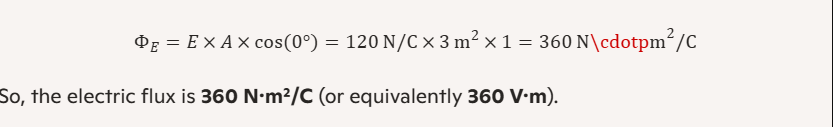
So, the electric flux is 360 N·m²/C (or equivalently 360 V·m).
Example 2: Tilted Surface
Now, consider the same electric field of 120 N/C and surface area of 3 m², but this time, the surface is tilted at 30° relative to the field direction. For 30°, the cosine value is approximately 0.866.

Even though the area and electric field are the same, the tilt reduces the effective flux to roughly 312 N·m²/C (or 312 V·m).
Why Understanding the Unit Matters
Dimensional Consistency
Understanding that electric flux is measured in N·m²/C ensures that when you work with laws like Gauss’s Law:
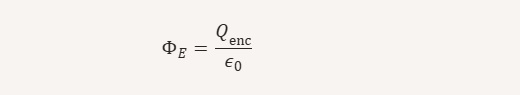
the units on both sides of the equation match. Here QencQ_{\text{enc}} is the charge (Coulomb) and ϵ0\epsilon_0 is the permittivity of free space (which has units C²/(N·m²)). This consistency is critical in physics to ensure that equations are valid.
Conceptual Clarity
When you understand that multiplying force per charge (N/C) by area (m²) gives you the flux unit (N·m²/C), you develop a stronger intuition about how electric fields interact with surfaces. This intuition is essential for solving problems in electrostatics and beyond.
Read More How to Clear NDA Exam In First Attempt
Practical Applications
- Classroom Problems: Whenever you’re solving problems related to electric fields, knowing the unit helps check your answers.
- Engineering: Electric flux calculations are vital in designing sensors, capacitors, and other electronic components.
Conclusion
The unit of electric flux—N·m²/C or V·m—is a concise representation of how an electric field interacts with a surface. By deriving it from the electric field (N/C or V/m) and the area (m²), we see why this unit is essential for ensuring that physical equations make sense dimensionally.
For students, mastering this unit is a critical step in understanding broader concepts in electromagnetism. With examples showing both perpendicular and tilted surfaces, you can see how different orientations of the area affect the electric flux. This solid understanding not only improves your problem-solving skills but also deepens your appreciation for the underlying principles of physics.




